An Introduction to Neural Networks
-
Prof. Leslie Smith
-
Centre for Cognitive and Computational
Neuroscience
-
Department of Computing and Mathematics
-
University of Stirling.
-
lss@cs.stir.ac.uk
-
last major update: 25 October 1996: minor update 22 April 1998 and 12 Sept 2001: links updated (they were really out of date) 12 Sept 2001; fix to math font (thanks Sietse Brouwer) 2 April 2003
- This page is also available in Swedish
This document is a roughly HTML-ised version of a talk given at the NSYN
meeting in Edinburgh, Scotland, on 28 February 1996, then updated a few times in response to comments received. Please email me comments,
but remember that this was originally just the slides from an introductory talk!
Overview:
Why would anyone want a `new' sort of computer?
What is a neural network?
Some algorithms and architectures.
Where have they been applied?
What new applications are likely?
Some useful sources of information.
Some comments added Sept 2001
NEW: questions and answers arising from this tutorial
Why would anyone want a `new' sort of computer?
What are (everyday) computer systems good at... .....and not so good at?
| Good at |
Not so good at |
| Fast arithmetic |
Interacting with noisy data or data from the environment |
| Doing precisely what the programmer programs
them to do |
Massive parallelism |
|
Massive parallelism |
|
Fault tolerance |
|
Adapting to circumstances |
Where can neural network systems help?
-
where we can't formulate an algorithmic solution.
-
where we can get lots of examples of the behaviour we require.
-
where we need to pick out the structure from existing data.
What is a neural network?
Neural Networks are a different paradigm for computing:
-
von Neumann machines are based on the processing/memory abstraction of
human information processing.
-
neural networks are based on the parallel architecture of animal brains.
Neural networks are a form of multiprocessor computer system, with
-
simple processing elements
-
a high degree of interconnection
-
simple scalar messages
-
adaptive interaction between elements
A biological neuron may have as many as 10,000 different inputs, and may
send its output (the presence or absence of a short-duration spike) to
many other neurons. Neurons are wired up in a 3-dimensional pattern.
Real brains, however, are orders of magnitude more complex than any
artificial neural network so far considered.
Example: A simple single unit adaptive network:
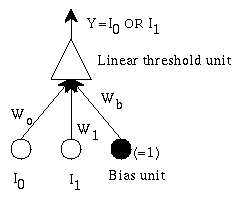
The network has 2 inputs, and one output. All are binary. The output
is
We want it to learn simple OR: output a 1 if either I0 or
I1 is 1.
Algorithms and Architectures.
The simple Perceptron:
The network adapts as follows: change the weight by an amount proportional
to the difference between the desired output and the actual output.
As an equation:
where is the learning rate, D is the desired output, and Y
is the actual output.
This is called the Perceptron Learning Rule, and goes back to
the early 1960's.
We expose the net to the patterns:
| I0 |
I1 |
Desired output |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
We train the network on these examples. Weights after each epoch
(exposure to complete set of patterns) 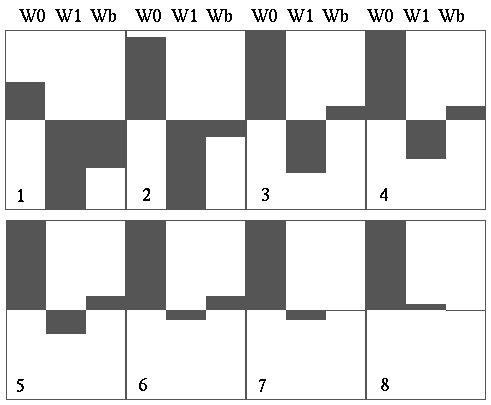
At this point (8) the network has finished learning. Since (D-Y)=0 for
all patterns, the weights cease adapting. Single perceptrons are limited
in what they can learn:
If we have two inputs, the decision surface is a line. ... and its equation
is
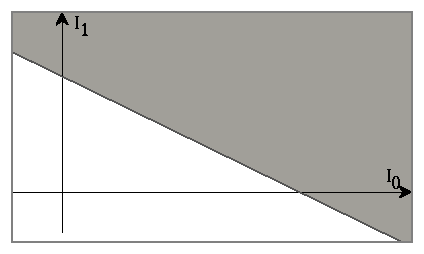
In general, they implement a simple hyperplane decision surface
This restricts the possible mappings available.
Developments from the simple perceptron:
Back-Propagated Delta Rule Networks (BP) (sometimes known and multi-layer
perceptrons (MLPs)) and Radial Basis Function Networks (RBF) are both well-known
developments of the Delta rule for single layer networks (itself a development
of the Perceptron Learning Rule). Both can learn arbitrary mappings or
classifications. Further, the inputs (and outputs) can have real values
Back-Propagated Delta Rule Networks (BP)
is a development from the simple Delta rule in which extra hidden layers
(layers additional to the input and output layers, not connected externally)
are added. The network topology is constrained to be feedforward:
i.e. loop-free - generally connections are allowed from the input layer
to the first (and possibly only) hidden layer; from the first hidden layer
to the second,..., and from the last hidden layer to the output layer.
Typical BP network architecture:
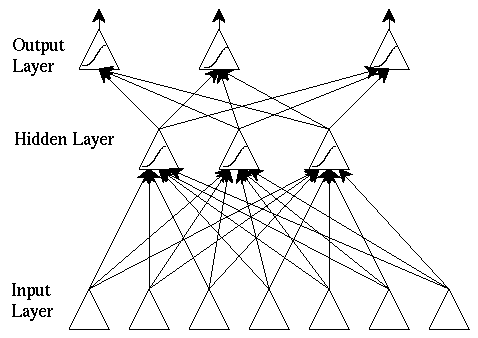
The hidden layer learns to recode (or to provide a representation
for) the inputs. More than one hidden layer can be used.
The architecture is more powerful than single-layer networks: it can
be shown that any mapping can be learned, given two hidden layers (of units).
The units are a little more complex than those in the original perceptron:
their input/output graph is
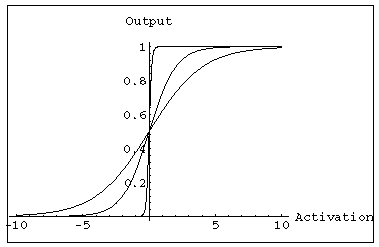
As a function:
The graph shows the output for k=0.5, 1, and 10, as the activation
varies from -10 to 10.
Training BP Networks
The weight change rule is a development of the perceptron learning rule.
Weights are changed by an amount proportional to the error at that unit
times the output of the unit feeding into the weight.
Running the network consists of
-
Forward pass:
-
the outputs are calculated and the error at the output units calculated.
-
Backward pass:
-
The output unit error is used to alter weights on the output units. Then
the error at the hidden nodes is calculated (by back-propagating
the error at the output units through the weights), and the weights on
the hidden nodes altered using these values.
For each data pair to be learned a forward pass and backwards pass is performed.
This is repeated over and over again until the error is at a low enough
level (or we give up).
Radial Basis function Networks
Radial basis function networks are also feedforward, but have only one
hidden layer.
Typical RBF architecture:
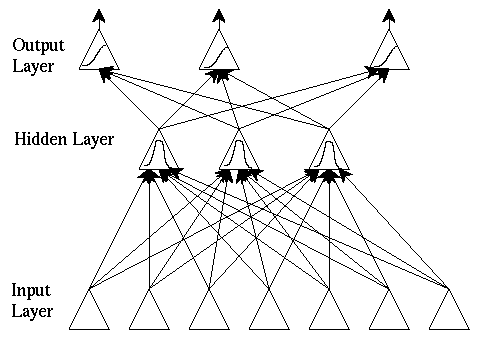
Like BP, RBF nets can learn arbitrary mappings: the primary difference
is in the hidden layer.
RBF hidden layer units have a receptive field which has a centre:
that is, a particular input value at which they have a maximal output.Their
output tails off as the input moves away from this point.
Generally, the hidden unit function is a Gaussian:
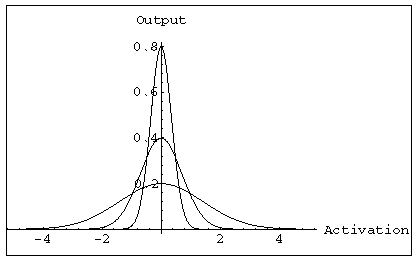
Gaussians with three different standard deviations.
Training RBF Networks.
RBF networks are trained by
-
deciding on how many hidden units there should be
-
deciding on their centres and the sharpnesses (standard deviation) of their
Gaussians
-
training up the output layer.
Generally, the centres and SDs are decided on first by examining the vectors
in the training data. The output layer weights are then trained using the
Delta rule. BP is the most widely applied neural network technique. RBFs
are gaining in popularity.
Nets can be
-
trained on classification data (each output represents one class), and
then used directly as classifiers of new data.
-
trained on (x,f(x)) points of an unknown function f, and then used to interpolate.
RBFs have the advantage that one can add extra units with centres near
parts of the input which are difficult to classify. Both BP and RBFs can
also be used for processing time-varying data: one can consider a window
on the data:
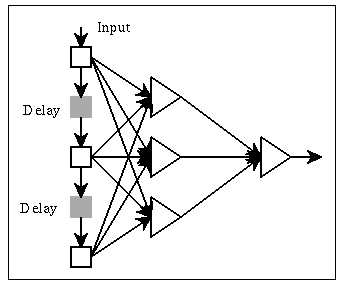
Networks of this form (finite-impulse response) have been used in many
applications.
There are also networks whose architectures are specialised for processing
time-series.
Unsupervised networks:
Simple Perceptrons, BP, and RBF networks need a teacher to tell the network
what the desired output should be. These are supervised networks.
In an unsupervised net, the network adapts purely in response to its
inputs. Such networks can learn to pick out structure in their input.
Applications for unsupervised nets
-
clustering data:
-
exactly one of a small number of output units comes on in response to an
input.
-
reducing the dimensionality of data:
-
data with high dimension (a large number of input units) is compressed
into a lower dimension (small number of output units).
Although learning in these nets can be slow, running the trained net is
very fast - even on a computer simulation of a neural net.
Kohonen clustering Algorithm:
- takes a high-dimensional input, and clusters it, but retaining some topological
ordering of the output.
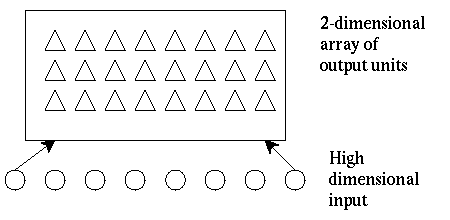
After training, an input will cause some the output units in
some area to become active.
Such clustering (and dimensionality reduction) is very useful as a preprocessing
stage, whether for further neural network data processing, or for more
traditional techniques.
Where are Neural Networks applicable?
..... or are they just a solution in search of a problem?
Neural networks cannot do anything that cannot be done using traditional
computing techniques, BUT they can do some things which would otherwise
be very difficult.
In particular, they can form a model from their training data (or possibly
input data) alone.
This is particularly useful with sensory data, or with data from a complex
(e.g. chemical, manufacturing, or commercial) process. There may be an
algorithm, but it is not known, or has too many variables. It is easier
to let the network learn from examples.
Neural networks are being used:
-
in investment analysis:
-
to attempt to predict the movement of stocks currencies etc., from previous
data. There, they are replacing earlier simpler linear models.
-
in signature analysis:
-
as a mechanism for comparing signatures made (e.g. in a bank) with those
stored. This is one of the first large-scale applications of neural networks
in the USA, and is also one of the first to use a neural network chip.
-
in process control:
-
there are clearly applications to be made here: most processes cannot be
determined as computable algorithms. Newcastle University Chemical Engineering
Department is working with industrial partners (such as Zeneca and BP)
in this area.
-
in monitoring:
-
networks have been used to monitor
-
the state of aircraft engines. By monitoring vibration levels and sound,
early warning of engine problems can be given.
-
British Rail have also been testing a similar application monitoring diesel
engines.
-
in marketing:
-
networks have been used to improve marketing mailshots. One technique is
to run a test mailshot, and look at the pattern of returns from this. The
idea is to find a predictive mapping from the data known about the clients
to how they have responded. This mapping is then used to direct further
mailshots.
To probe further:
A rather longer introduction (which is more commercially oriented) is hosted by StatSoft, Inc.
There is also another introduction (including some history) by Stergiou and Siganos.
The Natural Computing Applications Forum runs meetings (with attendees from
industry, commerce and academe) on applications of Neural Networks. Contact
NCAF through their website, by telephone +44 (0)1332 246989, or by fax +44 (0)1332 247129
Internet addresses:
NeuroNet which was at Kings College, London, was a European Network of Excellence in Neural
Networks which finished in March 2001. Howwever, their website remains a very useful source of information
IEEE Computational Intelligence Society (was IEEE Neural Networks Society) http://www.ieee-cis.org/ publish a number of journals on neural networks and related areas.
I wrote six lectures on Back Propagation rather a long time ago, in a now defunct WP. Still, they are readable...
Newscomp.ai.neural-nets has an very useful
set of frequently asked questions (FAQ's), available as a WWW document
at:
ftp://ftp.sas.com/pub/neural/FAQ.html
Courses
Quite a few organisations run courses: we used to run a 1 year Masters course in Neural Computation: unfortunately, this course in in abeyance.
We can even run courses to suit you. We are about to start up a centre in Computational Intelligence, called INCITE.
More Specific Information
Some further information about applications can be found from the book Stimulation
Initiative for European Neural Applications (SIENA).
For more information on Neural Networks in the Process Industries, try
A. Bulsari's home page .
The company BrainMaker has a nice list of references
on applications of its software package that shows the breadth of applications areas.
Journals.
The best journal for application-oriented information is
Neural Computing and Applications, Springer-Verlag. (address:
Sweetapple Ho, Catteshall Rd., Godalming, GU7 3DJ)
Books.
There's a lot of books on Neural Computing. See the FAQ
above for a much longer list.
For a not-too-mathematical introduction, try
Fausett L., Fundamentals of Neural Networks, Prentice-Hall, 1994.
ISBN 0 13 042250 9 or
Gurney K., An Introduction to Neural Networks, UCL Press, 1997,
ISBN 1 85728 503 4
Haykin S., Neural Networks , 2nd Edition, Prentice Hall, 1999, ISBN 0 13 273350 1 is a more detailed book, with excellent coverage of the whole subject.
Where are neural networks going?
A great deal of research is going on in neural networks worldwide.
This ranges from basic research into new and more efficient learning
algorithms, to networks which can respond to temporally varying patterns
(both ongoing at Stirling), to techniques for implementing neural networks
directly in silicon. Already one chip commercially available exists, but
it does not include adaptation. Edinburgh University have implemented a
neural network chip, and are working on the learning problem.
Production of a learning chip would allow the application of this technology
to a whole range of problems where the price of a PC and software cannot
be justified.
There is particular interest in sensory and sensing applications: nets
which learn to interpret real-world sensors and learn about their environment.
New Application areas:
-
Pen PC's
-
PC's where one can write on a tablet, and the writing will be recognised
and translated into (ASCII) text.
-
Speech and Vision recognition systems
-
Not new, but Neural Networks are becoming increasingly part of such systems.
They are used as a system component, in conjunction with traditional computers.
-
White goods and toys
-
As Neural Network chips become available, the possibility of simple cheap
systems which have learned to recognise simple entities (e.g. walls looming,
or simple commands like Go, or Stop), may lead to their incorporation in
toys and washing machines etc. Already the Japanese are using a related
technology, fuzzy logic, in this way. There is considerable interest in
the combination of fuzzy and neural technologies.
Reading this through, it is a bit outdated: not that there's anything incorrect above, but the world has moved on. Neural Networks should be seen as part of a larger field sometimes called Soft Computing or Natural Computing. In the last few years, there has been a real movement of the discipline in three different directions:
- Neural networks, statistics, generative models, Bayesian inference
- There is a sense in which these fields are coalescing. The real problem is making conclusions from incomplete, noisy data, and all of these fields offer something in this area. Developments in the mathematics underlying these fileds have shown that there are real similarities in the techniques used. Chris Bishop's book Neural Networks for Pattern Recognition, Oxford University Press is a good start on this area.
- Neuromorphic Systems
- Existing neural network (and indeed other soft computing) systems are generally software models for solving static problems on PCs. But why not free the concept from the workstation? The area of neuromorphic systems is concerned with real-time implementations of neurally inspired systems, generally implemented directly in silicon, for sensory and motor tasks. Another aspect is direct implementation of detailed aspects of neurons in silicon (see Biological Neural Networks below). The main centres worldwide are at the Institute for neuroinformatics at Zurich, and at the Center for Neuromorphic Systems Engineering at Caltech. There are also some useful links from the Institute for Neuromorphic Engineering. Indeed, the US DARPA has now discovered Neuromorphic Systems, and are funding research in this area (e.g. SyNAPSE).
- Biological Neural Networks
- There is real interest in how neural network research and neurophysiology can come together. The pattern recognition aspects of Artificial Neural Networks don't really explain too much about how real brains actually work. The field called Computational Neuroscience has taken inspiration from both artificial neural networks and neurophysiology, and attempts to put the two together.
Back to top of page
Back to Leslie Smith's home page
Last updated: Friday, 04-Aug-2017 16:52:03 BST
If you have any difficulties accessing this page, or you have any
queries/suggestions arising from this page, please email:
Prof Leslie S Smith (lss(nospam_please)@cs.stir.ac.uk)










